yuaida ho 87: Trigonometrische Funktionen

In der Mathematik wurden die trigonometrischen Funktionen (auch Kreisfunktionen genannt) Winkelfunktionen oder goniometrische Funktionen [19655004] [1] genannt. [2] ) sind Funktionen eines Winkels. Sie beziehen die Winkel eines Dreiecks auf die Länge der Seiten. Trigonometrische Funktionen sind unter anderem bei der Untersuchung von Dreiecken und der Modellierung periodischer Phänomene wichtig.

Die bekanntesten trigonometrischen Funktionen sind Sinus, Cosinus und Tangens. Im Zusammenhang mit dem Standardeinheitskreis (einem Kreis mit dem Radius 1 Einheit), bei dem ein Dreieck aus einem Strahl entsteht, der am Ursprung beginnt und mit der Achse $x$ dem Sinus des Winkels, einen Winkel bildet gibt die $y$ -Komponente (das Gegenteil des Winkels oder der Steigung) des Dreiecks an, der Cosinus gibt die $x$ -Komponente (die Nähe des Winkels oder des Laufs) an, und Die Tangentenfunktion gibt die Neigung an ( $y$ -Komponente geteilt durch die $x$ -Komponente). Bei Winkeln unter einem rechten Winkel werden trigonometrische Funktionen im Allgemeinen als Verhältnisse von zwei Seiten eines rechtwinkligen Dreiecks definiert, und ihre Werte können in den Längen verschiedener Liniensegmente um einen Einheitskreis gefunden werden. Moderne Definitionen drücken trigonometrische Funktionen als unendliche Reihen oder als Lösungen bestimmter Differentialgleichungen aus und ermöglichen die Erweiterung der Argumente auf die Ganzzahllinie und die komplexen Zahlen.

Trigonometrische Funktionen können vielfältig eingesetzt werden, einschließlich der Berechnung unbekannter Längen und Winkel in Dreiecken (häufig rechtwinkligen Dreiecken). In dieser Anwendung werden trigonometrische Funktionen beispielsweise in der Navigation, im Engineering und in der Physik verwendet. In der Elementarphysik wird häufig ein Vektor in kartesische Koordinaten aufgelöst. Die Sinus- und Cosinus-Funktionen werden auch häufig verwendet, um periodische Funktionsphänomene zu modellieren, wie etwa Schall- und Lichtwellen, die Position und Geschwindigkeit von harmonischen Oszillatoren, Sonnenlichtintensität und Tageslänge sowie durchschnittliche Temperaturschwankungen im Jahresverlauf.

Im modernen Gebrauch gibt es sechs trigonometrische Grundfunktionen, die hier in Tabellenform mit Gleichungen aufgeführt sind, die sie miteinander in Beziehung setzen. Insbesondere bei den letzten vier werden diese Beziehungen oft als Definitionen dieser Funktionen betrachtet, aber man kann sie ebenso gut geometrisch oder auf andere Weise definieren und dann diese Beziehungen ableiten.

Definitionen für rechtwinkliges Dreieck [ edit ]

Oben: Trigonometrische Funktion $sin θ$ für ausgewählte Winkel $θ$ [19456526] ] π - θ $π + θ$ und $2π - θ$ in den vier Quadranten.
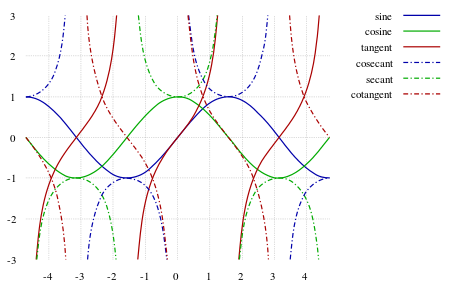
Unten: Graph der Sinusfunktion gegen den Winkel. Winkel von der oberen Tafel werden identifiziert.

Plot der sechs trigonometrischen Funktionen und des Einheitskreises für einen Winkel von 0,7 Radiant.

Die Vorstellung, dass es eine gewisse Übereinstimmung zwischen den Längen der Seiten eines Dreiecks und geben sollte Die Winkel des Dreiecks kommen, sobald man erkennt, dass ähnliche Dreiecke die gleichen Verhältnisse zwischen ihren Seiten beibehalten. Das heißt, für jedes ähnliche Dreieck bleibt das Verhältnis der Hypotenuse (zum Beispiel) und einer anderen der Seiten gleich. Ist die Hypotenuse doppelt so lang, so sind die Seiten. Diese Verhältnisse drücken die trigonometrischen Funktionen aus.
Zum Definieren der trigonometrischen Funktionen für den Winkel A beginnen Sie mit einem beliebigen rechten Dreieck, das den Winkel enthält A . Die drei Seiten des Dreiecks werden wie folgt benannt:

Die Hypotenuse ist die dem rechten Winkel gegenüberliegende Seite, in diesem Fall die Seite h . Die Hypotenuse ist immer die längste Seite eines rechtwinkligen Dreiecks.

Die gegenüberliegende Seite ist die Seite, die dem Winkel gegenüberliegt, an dem wir interessiert sind (Winkel A ) Fallseite a .

Die benachbarte Seite ist die Seite, die sowohl die interessierenden Winkel (Winkel A ) als auch den rechten Winkel C aufweist ]), in diesem Fall side b .
In gewöhnlicher euklidischer Geometrie betragen die Innenwinkel jedes Dreiecks nach dem Dreieckspostulat 180 ° ( $π$ radians). Daher sind in einem rechtwinkligen Dreieck die beiden nicht rechten Winkel insgesamt 90 ° ( $π$ / 2 Radianten), so dass jeder dieser Winkel im Bereich von $liegen muss ] (0, π / 2)$ ausgedrückt in Intervallnotation. Die folgenden Definitionen gelten für Winkel in diesem Bereich von $(0, π / 2)$ . Sie können durch Verwendung des Einheitskreises auf den gesamten Satz reeller Argumente erweitert werden, oder indem bestimmte Symmetrien erforderlich sind und es sich um periodische Funktionen handelt. Beispielsweise zeigt die Figur $sin (θ)$ für Winkel $θ$ $π -$ + θ und $2 π - θ$ dargestellt auf dem Einheitskreis (oben) und als Grafik (unten). Der Wert des Sinus wiederholt sich abgesehen vom Vorzeichen in allen vier Quadranten, und wenn der Bereich von $θ$ um zusätzliche Rotationen erweitert wird, wiederholt sich dieses Verhalten periodisch mit einer Periode 2 $π$ .
Die trigonometrischen Funktionen sind in der folgenden Tabelle zusammengefasst und im Folgenden näher beschrieben. Der Winkel $θ$ ist der Winkel zwischen der Hypotenuse und der benachbarten Linie - der Winkel bei A im beiliegenden Diagramm.

Sinus, Cosinus und Tangens [ edit ]

Der Winkel eines Winkels ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der Hypotenuse. Das Wort stammt aus dem lateinischen Sinus für Golf oder Bucht, ^[3]da es sich bei einem Einheitskreis um die Seite des Dreiecks handelt, auf der sich der Winkel öffnet. . In unserem Fall:

${displaystyle sin A={frac {textrm {opposite}}{textrm {hypotenuse}}}}$

Ein Beispiel für die Beziehung zwischen Sinus und seinem Out-of-Phase-Komplement Cosinus Cosinus ist identisch, aber $π$ / 2 ist nach rechts außer Phase; so $cos A = sin (A + π / 2)$ . Der Cosinus ( Sinus Complement Latein: Cosinus Sinus Complementi ) eines Winkels ist das Verhältnis der Länge des benachbarte Seite der Länge der Hypotenuse, so genannt, weil sie der Sinus des Komplementär- oder Ko-Winkels ist, der andere nicht rechte Winkel. ^[4] Da die Winkelsumme eines Dreiecks $π$ Radiant ist, ist der Ko-Winkel $B$ gleich $π / 2 . A$ ; so ${displaystyle cos A={frac {textrm {adjacent}}{textrm {hypotenuse}}}}$
Der Tangent eines Winkels ist das Verhältnis von die Länge der gegenüberliegenden Seite zur Länge der benachbarten Seite, so genannt, weil sie als Liniensegment tangential zum Kreis dargestellt werden kann, dh die Linie, die den Kreis berührt, aus lateinischer Linie linea tangens [19459016oderberührendeLinie(vgl tangere zum Anfassen). ^[5] In unserem Fall:

${ displaystyle tan A = { frac { textrm {gegenüberliegend}} { textrm {angrenzend}}}}$
Tangent kann auch als Sinus und Cosinus dargestellt werden. Das ist:

${displaystyle tan A={frac {sin A}{cos A}}={frac {frac {textrm {opposite}}{textrm {hypotenuse}}}{frac {textrm {adjacent}}{textrm {hypotenuse}}}}={frac {textrm {opposite}}{textrm {adjacent}}}}$
Diese Verhältnisse hängen nicht ab von der Größe des bestimmten gewählten rechten Dreiecks, solange der Fokuswinkel gleich ist, da alle derartigen Dreiecke ähnlich sind.
Die Akronyme "SOH-CAH-TOA" ("einweichen-a-toe", "sock-a-toa", "so-kah-toa") und "OHSAHCOAT" sind für diese Verhältnisse üblicherweise verwendete trigonometrische Mnemonik.

Secant, Cosecant und Cotangens [ edit ]

Die verbleibenden drei Funktionen lassen sich am besten anhand der drei oben genannten Funktionen definieren und können als deren wechselseitige Funktion betrachtet werden.
Der Winkel eines Winkels ist der Kehrwert seines Cosinus, d. H. Das Verhältnis der Länge der Hypotenuse zur Länge der benachbarten Seite, weil sie so genannt wird stellt die Sekantenlinie dar, die den Kreis schneidet (aus dem Lateinischen: secare um zu schneiden): ^{[6] 19659119] sec ⁡ A A ] = 1 cos 19 A = Hypotenuse benachbart = h b . displaystyle sec A = { frac {1} { cos A}} = { frac { textrm {hypotenuse}} { textrm {angrenzend}}}} = { frac {h} {b}}.}} $sec A = { frac {1} { cos A}} = { frac { textrm {hypotenuse}} { textrm {angrenzend}}} = { frac {h} {b}}.$
Der Cosecant () Sekantenergänzung Latein: Cosecans secans Complementi ) von einem Winkel ist der Kehrwert seines Sinus, das heißt der ra tio der Länge der Hypotenuse auf die Länge der gegenüberliegenden Seite, so genannt, weil sie die Sekante des Komplementär- oder Kowinkels ist:

${ displaystyle csc A = { frac {1} { sin A}} = { frac { textrm {hypotenuse}} { textrm {Gegenteil}} } = { frac {h} {a}}.}$
Der cotangent ( tangentiale Ergänzung lateinisch: cotangens tangens Complementi ) eines Winkels ist der Kehrwert seiner Tangente, dh das Verhältnis der Länge der benachbarten Seite zur Länge der gegenüberliegenden Seite, so genannt, weil es die Tangente der Komplementärart ist oder Co-Winkel:

${displaystyle cot A={frac {1}{tan A}}={frac {textrm {adjacent}}{textrm {opposite}}}={frac {b}{a}}.}$
Mnemonics [ edit ]

Äquivalent zu den Definitionen des rechtwinkligen Dreiecks können die trigonometrischen Funktionen auch als Anstieg Lauf und Steigung eines Liniensegments definiert werden relativ zur Horizontalen. Die Neigung wird allgemein als "Anstieg über die Läufe" oder Anstieg / Lauf gelehrt. Die drei trigonometrischen Hauptfunktionen werden im Allgemeinen in der Reihenfolge Sinus, Cosinus und Tangens unterrichtet. Bei einer Liniensegmentlänge von 1 (wie in einem Einheitskreis) zeigen die folgenden mnemonischen Geräte die Entsprechung der Definitionen:

"Sinus ist zuerst, Anstieg ist zuerst", was bedeutet, dass Sinus den Winkel des Liniensegments annimmt und seinen vertikalen Anstieg angibt, wenn die Länge der Linie 1 ist.

"Cosinus ist Sekunde, Lauf ist Sekunde" bedeutet dies Cosinus nimmt den Winkel des Liniensegments und teilt ihm seinen horizontalen Verlauf mit, wenn die Länge der Linie 1 ist.

"Tangent kombiniert Steigen und Laufen", was bedeutet, dass Tangent den Winkel des Liniensegments nimmt und seine Neigung angibt, oder alternativ , gibt den vertikalen Anstieg an, wenn der horizontale Verlauf des Liniensegments 1 ist.
Dies zeigt die hauptsächliche Verwendung von Tangens und Arkustangens: Umwandlung zwischen den beiden Arten, die Neigung einer Linie zu erklären, dh Winkel und Steigungen. (Der Arkustangens oder "inverse Tangens" ist nicht mit dem Cotangens zu verwechseln, bei dem es sich um einen durch Sinus getrennten Cosinus handelt.)
Während die Länge des Liniensegments für die Steigung keine Rolle spielt (die Steigung hängt nicht von der Länge der geneigten Linie ab), beeinflusst sie jedoch den Anstieg und den Lauf. Um den tatsächlichen Anstieg und Verlauf anzupassen, wenn die Linie nicht die Länge 1 hat, multiplizieren Sie einfach den Sinus und den Cosinus mit der Leitungslänge. Wenn das Liniensegment beispielsweise die Länge 5 hat, beträgt der Lauf unter einem Winkel von 7 ° 5cos (7 °).

Definition von Einheitskreis [ edit ]

In dieser Abbildung sind die sechs trigonometrischen Funktionen eines beliebigen Winkels $θ$ als kartesische Koordinaten von Punkten dargestellt, die sich auf den Einheitskreis beziehen. Die Ordinaten von $A$ $B$ und $D$ sind $sin θ$ $tan tan [1945650101]. und csc θ während die Abszissen von A C und E cos waren. θ$ $cot θ$ und $sec θ$

Zeichen von trigonometrischen Funktionen in jedem Quadranten. Die Mnemonik " all s cience t jeder (die) c razy" listet die Funktionen auf, die von den Quadranten I bis IV positiv sind. ^[7] Dies ist eine Variation der Mnemonik "All Students Take Calculus".

Die sechs trigonometrischen Funktionen können als Koordinatenwerte von Punkten auf der euklidischen Ebene definiert werden, die sich auf den Einheitskreis beziehen, bei dem es sich um den Radius handelt, der um einen Mittelpunkt zentriert ist der Ursprung $O$ dieses Koordinatensystems. Definitionen für rechtwinklige Dreiecke erlauben die Definition der trigonometrischen Funktionen für Winkel zwischen $0$ und ${displaystyle {tfrac {pi }{2}}}$ radian $(90 °),$ Die Einheitskreisdefinitionen erlauben es, den Bereich der trigonometrischen Funktionen auf alle positiven und negativen reellen Zahlen zu erweitern.
Drehen eines Strahls aus der Richtung der positiven Hälfte der Achse x um einen Winkel $θ$ (entgegen dem Uhrzeigersinn für ${ displaystyle theta> 0,}$ und im Uhrzeigersinn für ${[display65] theta <0}$ ) ergibt Schnittpunkte dieses Strahls (siehe Abbildung). mit dem Einheitskreis : ${ displaystyle mathrm {A} = (x _ { mathrm {A}}, y _ { mathrm {A}})}$ und durch Erweitern des Strahls auf eine Linie, falls erforderlich, mit dem line ${19659134] { displaystyle {}} x = 1 { text {”}}: ; mathrm {B} = (x _ { mathrm {B}}, y _ { mathrm {B}}),}$
Die trigonometrischen Funktionen $cos$ und $sin$ werden jeweils als x - und y -koordinierte Werte des Punktes [] definiert. $A$ dh

${ displaystyle quad sin ( theta) = y _ { mathrm {A}}.}$ [8]
Im Bereich ${19659217] {19659217] {19659217] {19659217]$ Diese Definition stimmt mit der Definition des rechtwinkligen Dreiecks durch überein unter Verwendung des rechtwinkligen Dreiecks, um den Einheitsradius $OA$ als Hypotenuse zu erhalten, und da für alle Punkte ${ displaystyle mathrm {P} = (x, y)}$ auf dem Einheitskreis der Gleichung ${ displaystyle x ^ {2} + y ^ {2} = 1}$

${ displaystyle cos ^ {2} theta + sin ^ {2} theta = 1 .}$
Die anderen trigonometrischen Funktionen können entlang des Einheitskreises als gefunden werden

${ displaystyle quad cot ( theta) = x _ { mathrm {C}}}}$

$d d d { displaystyle csc ( theta) = y _ { mathrm {D}} quad}$ und ${ displaystyle quad sec ( theta) = x _ { mathrm {E}}.}$
Durch die Anwendung der Pythagorean-Identitäts- und geometrischen Beweismethoden können diese Definitionen leicht mit den Definitionen von Tangens, Cotangens, Sekante und Cosecans in Bezug auf Sinus übereinstimmen und Cosinus, das ist

${ displaystyle tan theta = { frac { sin theta} { cos theta}}, quad cot theta = { frac { cos theta} { sin theta}, quad sec theta = { frac {1} { cos theta}}, quad csc theta = { frac {1} { sin theta}}.}$

Trigonometrische Funktionen: Sine Cosine Tangent Secant (gepunktet) Cotangent (gepunktet)

Als Drehung eines Winkels von ${ displaystyle pm 2 pi}$ ändert das nicht Position oder Größe einer Form sind die Punkte $A$ $B$ $C$ $D$ und $E$ das gleiche gilt für zwei Winkel, deren Differenz ein ganzzahliges Vielfaches von ${ displaystyle 2 pi}$ . Trigonometrische Funktionen sind also periodische Funktionen mit Perioden $[Displaystyle2pi}$ . Das sind die Gleichheiten

${ displaystyle sin theta = sin left ( theta + 2k pi right) quad }$ und ${ displaystyle quad cos theta = cos left ( theta + 2k pi right)}$
gilt für jeden Winkel $θ$ und eine beliebige ganze Zahl $k$ . Gleiches gilt für die vier anderen trigonometrischen Funktionen. Die Beobachtung des Zeichens und der Monotonie der Funktionen Sinus, Cosinus, Cosecant und Sekante in den vier Quadranten zeigt, dass $2 π$ der kleinste Wert ist, für den sie periodisch sind, dh $2 π$ ist die grundlegende Periode dieser Funktionen. Jedoch bereits nach einer Drehung um einen Winkel ${ displaystyle pi}$ die Punkte $B$ und $C$ kehren in ihre ursprüngliche Position zurück, so dass die Tangensfunktion und die Kotangensfunktion eine grundlegende Periode von $π$ haben. Das sind die Gleichheiten

${ displaystyle tan theta = tan ( theta + k pi) quad}$ und ${ displaystyle quad cot theta = cot ( theta + k pi)}$
gilt für jeden Winkel $θ$ und jede ganze Zahl $k$ .

Algebraische Werte [ edit ]

Der Einheitskreis mit einigen Punkten, die mit Cosinus und Sinus (in dieser Reihenfolge) und den entsprechenden Winkeln in Radiant und Grad gekennzeichnet sind.

The algebraische Ausdrücke für $sin (0 °), sin (30 °), sin (45 °), sin (60 °)$ und $sin (90 °)$ sind

${displaystyle 0,quad {frac {1}{2}},quad {frac {sqrt {2}}{2}},quad {frac {sqrt {3}}{2}},quad 1,,!}$
. Schreiben der Zähler als Quadratwurzeln aufeinanderfolgender natürlicher Zahlen ( ${displaystyle {tfrac {sqrt {0}}{2}},{tfrac {sqrt {1}}{2}},{tfrac {sqrt {2}}{2}},{tfrac {sqrt {3}}{2}},{tfrac {sqrt {4}}{2}}}$ [19456580] { displaystyle { tfrac { sqrt {0}} {2}}, { tfrac { sqrt {1}} {2}}, { tfrac { sqrt {2}} {2}}, { tfrac { sqrt {3}} {2}}, { tfrac { sqrt {4}} {2}} ${ displaystyle { tfrac { sqrt {0}} {2} }, { tfrac { sqrt {1}} {2}}, { tfrac { sqrt {2}} {2}}, { tfrac { sqrt {3}} {2}}, { tfrac { sqrt {4}} {2}}$ ) stellt eine einfache Möglichkeit dar, sich die Werte zu merken. ^[9]
Solche einfachen Ausdrücke existieren im Allgemeinen nicht für andere Winkel, die rationale Vielfache von a sind geraden Winkel.
Für einen Winkel, der in Grad gemessen ein Vielfaches von drei ist, können Sinus und Cosinus in Form von Quadratwurzeln ausgedrückt werden, wie nachstehend gezeigt. Diese Werte für Sinus und Cosinus können somit durch Lineal und Kompass konstruiert werden.
Für einen Winkel einer ganzzahligen Gradzahl können Sinus und Cosinus in Form von Quadratwurzeln und der Kubikwurzel eines Nicht-Real ausgedrückt werden komplexe Nummer . Die Galois-Theorie erlaubt den Beweis, dass nicht-echte Würfelwurzeln unvermeidbar sind, wenn der Winkel kein Vielfaches von 3 ° ist.
Für einen Winkel, der in Grad gemessen eine rationale Zahl von ist, sind Sinus und Cosinus algebraische Zahlen die als $n ausgedrückt werden können.$ th Wurzeln . Dies resultiert aus der Tatsache, dass die Galois-Gruppen der cyclotomischen Polynome cyclisch sind.
For an angle which, measured in degrees, is not a rational number, then either the angle or both the sine and the cosine are transcendental numbers. This is a corollary of Baker's theoremproved in 1966.

Explicit values[edit]

Algebraic expressions for 15°, 18°, 36°, 54°, 72° and 75° are as follows:

${displaystyle sin 15^{circ }=cos 75^{circ }={frac {{sqrt {6}}-{sqrt {2}}}{4}},!}$

${displaystyle sin 18^{circ }=cos 72^{circ }={frac {{sqrt {5}}-1}{4}}}$

${displaystyle sin 36^{circ }=cos 54^{circ }={frac {sqrt {10-2{sqrt {5}}}}{4}}}$

${displaystyle sin 54^{circ }=cos 36^{circ }={frac {{sqrt {5}}+1}{4}},!}$

${displaystyle sin 72^{circ }=cos 18^{circ }={frac {sqrt {10+2{sqrt {5}}}}{4}}}$

${displaystyle sin 75^{circ }=cos 15^{circ }={frac {{sqrt {6}}+{sqrt {2}}}{4}}.,}$
From these, the algebraic expressions for all multiples of 3° can be computed. Zum Beispiel:

${displaystyle sin 3^{circ }=cos 87^{circ }={frac {2left(1-{sqrt {3}}right){sqrt {5+{sqrt {5}}}}+left(1+{sqrt {3}}right)left({sqrt {10}}-{sqrt {2}}right)}{16}},!}$

${displaystyle sin 6^{circ }=cos 84^{circ }={frac {{sqrt {30-6{sqrt {5}}}}-{sqrt {5}}-1}{8}},!}$

${displaystyle sin 9^{circ }=cos 81^{circ }={frac {{sqrt {10}}+{sqrt {2}}-2{sqrt {5-{sqrt {5}}}}}{8}},!}$

${displaystyle sin 84^{circ }=cos 6^{circ }={frac {{sqrt {10-2{sqrt {5}}}}+{sqrt {3}}+{sqrt {15}}}{8}}}$

${displaystyle sin 87^{circ }=cos 3^{circ }={frac {2left(1+{sqrt {3}}right){sqrt {5+{sqrt {5}}}}-left(1-{sqrt {3}}right)left({sqrt {10}}-{sqrt {2}}right)}{16}}.}$
Algebraic expressions can be deduced for other angles of an integer number of degrees, for example,

${displaystyle sin 1^{circ }={frac {{sqrt[{3}]{z}}-{dfrac {1}{sqrt[{3}]{z}}}}{2i}},}$
where $z = a + ib$ and $a$ and $b$ are the above algebraic expressions for, respectively, $cos 3°$ and $sin 3°$ and the principal cube root (that is, the cube root with the largest real part) is to be taken.

Series definitions[edit]

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.

Animation for the approximation of cosine via Taylor polynomials.

${displaystyle cos(x)}$ together with the first Taylor polynomials ${displaystyle p_{n}(x)=sum _{k=0}^{n}(-1)^{k}{frac {x^{2k}}{(2k)!}}}$

Trigonometric functions are analytic functions. Using only geometry and properties of limitsit can be shown that the derivative of sine is cosine and the derivative of cosine is the negative of sine. One can then use the theory of Taylor series to show that the following identities hold for all real numbers $x$ .^[10] Here, and generally in calculusall angles are measured in radians.

${displaystyle {begin{aligned}sin x&=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots \&=sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\end{aligned}}}$
${displaystyle {begin{aligned}cos x&=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-{frac {x^{6}}{6!}}+cdots \&=sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n}}{(2n)!}}end{aligned}}}$
The infinite series appearing in these identities are convergent in the whole complex plane and are often taken as the definitions of the sine and cosine functions of a complex variable. Another standard (and equivalent) definition of the sine and the cosine as functions of a complex variable is through their differential equationbelow.
Other series can be found.^[11] For the following trigonometric functions:

$U n$ is the $n$ th up/down number,

$B n$ is the $n$ th Bernoulli numberand

$E n$ (below) is the $n$ th Euler number.
${displaystyle {begin{aligned}tan x&{}=sum _{n=0}^{infty }{frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\&{}=sum _{n=1}^{infty }{frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\&{}=x+{frac {1}{3}}x^{3}+{frac {2}{15}}x^{5}+{frac {17}{315}}x^{7}+cdots ,qquad {text{for }}|x|<{frac {pi }{2}}.end{aligned}}}$
${displaystyle {begin{aligned}csc x&{}=sum _{n=0}^{infty }{frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\&{}=x^{-1}+{frac {1}{6}}x+{frac {7}{360}}x^{3}+{frac {31}{15120}}x^{5}+cdots ,qquad {text{for }}0<|x|<pi .end{aligned}}}$
${displaystyle {begin{aligned}sec x&{}=sum _{n=0}^{infty }{frac {U_{2n}x^{2n}}{(2n)!}}=sum _{n=0}^{infty }{frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\&{}=1+{frac {1}{2}}x^{2}+{frac {5}{24}}x^{4}+{frac {61}{720}}x^{6}+cdots ,qquad {text{for }}|x|<{frac {pi }{2}}.end{aligned}}}$
${displaystyle {begin{aligned}cot x&{}=sum _{n=0}^{infty }{frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\&{}=x^{-1}-{frac {1}{3}}x-{frac {1}{45}}x^{3}-{frac {2}{945}}x^{5}-cdots ,qquad {text{for }}0<|x|<pi .end{aligned}}}$
When the series for the tangent and secant functions are expressed in a form in which the denominators are the corresponding factorials, the numerators, called the "tangent numbers" and "secant numbers" respectively, have a combinatorial interpretation: they enumerate alternating permutations of finite sets, of odd cardinality for the tangent series and even cardinality for the secant series.^[12] The series itself can be found by a power series solution of the aforementioned differential equation.
From a theorem in complex analysisthere is a unique analytic continuation of this real function to the domain of complex numbers. They have the same Taylor series, and so the trigonometric functions are defined on the complex numbers using the Taylor series above.
There is a series representation as partial fraction expansion where just translated reciprocal functions are summed up, such that the poles of the cotangent function and the reciprocal functions match:^[13]

${displaystyle pi cdot cot(pi x)=lim _{Nto infty }sum _{n=-N}^{N}{frac {1}{x+n}}.}$
This identity can be proven with the Herglotz trick.^[14]
Combining the $(- n)$ th with the $n$ th term lead to absolutely convergent series:

${displaystyle pi cdot cot(pi x)={frac {1}{x}}+sum _{n=1}^{infty }{frac {2x}{x^{2}-n^{2}}} ,quad {frac {pi }{sin(pi x)}}={frac {1}{x}}+sum _{n=1}^{infty }{frac {(-1)^{n},2x}{x^{2}-n^{2}}}.}$
Relationship to exponential function and complex numbers[edit]

${displaystyle cos(theta )}$ and ${displaystyle sin(theta )}$ are the real and imaginary part of ${displaystyle mathrm {e} ^{mathrm {i} theta }}$ respectively.

It can be shown from the series definitions^[15] that the sine and cosine functions are respectively the imaginary and real parts of the exponential function of a purely imaginary argument. That is, if $x$ is real, we have

${displaystyle cos x=operatorname {Re} (e^{ix}),,qquad sin x=operatorname {Im} (e^{ix}),,}$
and

${displaystyle e^{ix}=cos x+isin x,.}$
The latter identity, although primarily established for real $x$ remains valid for every complex $x$ and is called Euler's formula.
Euler's formula can be used to derive most trigonometric identities from the properties of the exponential function, by writing sine and cosine as:

${displaystyle sin x={frac {e^{ix}-e^{-ix}}{2i}},,qquad cos x={frac {e^{ix}+e^{-ix}}{2}},.}$
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of their arguments.

${displaystyle {begin{aligned}sin(x+iy)&=sin xcosh y+icos xsinh y,,\cos(x+iy)&=cos xcosh y-isin xsinh y,.end{aligned}}}$
This exhibits a deep relationship between the complex sine and cosine functions and their real (sin, cos) and hyperbolic real (sinh cosh) counterparts.

Complex graphs[edit]

In the following graphs the domain is the complex plane pictured with domain coloringand the range values are indicated at each point by color. Brightness indicates the size (absolute value) of the range value, with black being zero. Hue varies with argument, or angle, measured from the positive real axis.

Definitions via differential equations[edit]

Both the sine and cosine functions satisfy the linear differential equation:

${displaystyle y''=-y,.}$
That is to say, each is the additive inverse of its own second derivative. Within the 2-dimensional function space $V$ consisting of all solutions of this equation,

the sine function is the unique solution satisfying the initial condition ${displaystyle left(y'(0),y(0)right)=(1,0),}$ and

the cosine function is the unique solution satisfying the initial condition ${displaystyle left(y'(0),y(0)right)=(0,1),}$ .
Since the sine and cosine functions are linearly independent, together they form a basis of $V$ . This method of defining the sine and cosine functions is essentially equivalent to using Euler's formula. (See linear differential equation.) It turns out that this differential equation can be used not only to define the sine and cosine functions but also to prove the trigonometric identities for the sine and cosine functions.
Further, the observation that sine and cosine satisfies $y ″ = - y$ means that they are eigenfunctions of the second-derivative operator.
The tangent function is the unique solution of the nonlinear differential equation

${displaystyle y'=1+y^{2},}$
satisfying the initial condition $y (0) = 0$ . There is a very interesting visual proof that the tangent function satisfies this differential equation.^[16]

The significance of radians[edit]

Radians specify an angle by measuring the length around the path of the unit circle and constitute a special argument to the sine and cosine functions. In particular, only sines and cosines that map radians to ratios satisfy the differential equations that classically describe them. If an argument to sine or cosine in radians is scaled by frequency,

${displaystyle f(x)=sin(kx),,}$
then the derivatives will scale by amplitude.

${displaystyle f'(x)=kcos(kx).,}$
Here, $k$ is a constant that represents a mapping between units. If $x$ is in degrees, then

${displaystyle k={frac {pi }{180^{circ }}}.}$
This means that the second derivative of a sine in degrees does not satisfy the differential equation

${displaystyle y''=-y,}$
but rather

${displaystyle y''=-k^{2}y.,}$
The cosine's second derivative behaves similarly.
This means that these sines and cosines are different functions, and that the fourth derivative of sine will be sine again only if the argument is in radians.

Identities[edit]

Many identities interrelate the trigonometric functions. Among the most frequently used is the Pythagorean identitywhich states that for any angle, the square of the sine plus the square of the cosine is 1. This is easy to see by studying a right triangle of hypotenuse 1 and applying the Pythagorean theorem. In symbolic form, the Pythagorean identity is written

${displaystyle sin ^{2}x+cos ^{2}x=1}$
which is standard shorthand notation for

${displaystyle (sin x)^{2}+(cos x)^{2}=1.}$
Other key relationships are the sum and difference formulaswhich give the sine and cosine of the sum and difference of two angles in terms of sines and cosines of the angles themselves. These can be derived geometrically, using arguments that date to Ptolemy. One can also produce them algebraically using Euler's formula.

Sum

${displaystyle {begin{aligned}sin left(x+yright)&=sin xcos y+cos xsin y,\cos left(x+yright)&=cos xcos y-sin xsin y,end{aligned}}}$

Difference

${displaystyle {begin{aligned}sin left(x-yright)&=sin xcos y-cos xsin y,\cos left(x-yright)&=cos xcos y+sin xsin y.end{aligned}}}$
These in turn lead to the following three-angle formulae:

${displaystyle {begin{aligned}sin left(x+y+zright)&=sin xcos ycos z+sin ycos zcos x+sin zcos ycos x-sin xsin ysin z,\cos left(x+y+zright)&=cos xcos ycos z-cos xsin ysin z-cos ysin xsin z-cos zsin xsin y,end{aligned}}}$
When the two angles are equal, the sum formulas reduce to simpler equations known as the double-angle formulae.

${displaystyle {begin{aligned}sin left(2xright)&=2sin xcos x,\cos left(2xright)&=cos ^{2}x-sin ^{2}x=2cos ^{2}x-1=1-2sin ^{2}x.end{aligned}}}$
When three angles are equal, the three-angle formulae simplify to

${displaystyle {begin{aligned}sin(3x)&=3sin x-4sin ^{3}x.\cos(3x)&=4cos ^{3}x-3cos x.end{aligned}}}$
These identities can also be used to derive the product-to-sum identities that were used in antiquity to transform the product of two numbers into a sum of numbers and greatly speed operations, much like the logarithm function.

Calculus[edit]

For integrals and derivatives of trigonometric functions, see the relevant sections of Differentiation of trigonometric functions Lists of integrals and List of integrals of trigonometric functions. Below is the list of the derivatives and integrals of the six basic trigonometric functions. The number $C$ is a constant of integration.

${displaystyle {begin{array}{|r|rr|}f(x)&f'(x)&int f(x),dx\hline sin x&cos x&-cos x+C\cos x&-sin x&sin x+C\tan x&sec ^{2}x=1+tan ^{2}x&-ln left|cos xright|+C\cot x&-csc ^{2}x=-(1+cot ^{2}x)&ln left|sin xright|+C\sec x&sec xtan x&ln left|sec x+tan xright|+C\csc x&-csc xcot x&-ln left|csc x+cot xright|+Cend{array}}}$
Definitions using functional equations[edit]

In mathematical analysisone can define the trigonometric functions using functional equations based on properties like the difference formula. Taking as given these formulas, one can prove that only two continuous functions satisfy those conditions. Formally, there exists exactly one pair of continuous functions—sin and cos—such that for all real numbers $x$ and $y$ the following equation holds:^[17]

${displaystyle cos(x-y)=cos xcos y+sin xsin y,}$
with the added condition that

${displaystyle 0<xcos x<sin x<xquad {text{ for }}quad 0<x<1.,}$
This may also be used for extending sine and cosine to the complex numbers. Other functional equations are also possible for defining trigonometric functions.

Computation[edit]

The computation of trigonometric functions is a complicated subject, which can today be avoided by most people because of the widespread availability of computers and scientific calculators that provide built-in trigonometric functions for any angle. This section, however, describes details of their computation in three important contexts: the historical use of trigonometric tables, the modern techniques used by computers, and a few "important" angles where simple exact values are easily found.
The first step in computing any trigonometric function is range reduction—reducing the given angle to a "reduced angle" inside a small range of angles, say 0 to $π$ /2using the periodicity and symmetries of the trigonometric functions.

Prior to computers, people typically evaluated trigonometric functions by interpolating from a detailed table of their values, calculated to many significant figures. Such tables have been available for as long as trigonometric functions have been described (see History below), and were typically generated by repeated application of the half-angle and angle-addition identities starting from a known value (such as sin( $π$ /2) = 1).
Modern computers use a variety of techniques.^[18] One common method, especially on higher-end processors with floating point units, is to combine a polynomial or rational approximation (such as Chebyshev approximationbest uniform approximation, and Padé approximationand typically for higher or variable precisions, Taylor and Laurent series) with range reduction and a table lookup—they first look up the closest angle in a small table, and then use the polynomial to compute the correction.^[19] Devices that lack hardware multipliers often use an algorithm called CORDIC (as well as related techniques), which uses only addition, subtraction, bitshiftand table lookup. These methods are commonly implemented in hardware floating-point units for performance reasons.
For very high precision calculations, when series expansion convergence becomes too slow, trigonometric functions can be approximated by the arithmetic-geometric meanwhich itself approximates the trigonometric function by the (complex) elliptic integral.^[20]

Finally, for some simple angles, the values can be easily computed by hand using the Pythagorean theoremas in the following examples. For example, the sine, cosine and tangent of any integer multiple of $π$ /60 radians (3°) can be found exactly by hand.
Consider a right triangle where the two other angles are equal, and therefore are both $π$ /4 radians (45°). Then the length of side $b$ and the length of side $a$ are equal; we can choose $a = b = 1$ . The values of sine, cosine and tangent of an angle of $π$ /4 radians (45°) can then be found using the Pythagorean theorem:

${displaystyle c={sqrt {a^{2}+b^{2}}}={sqrt {2}},.}$
Therefore:

${displaystyle sin {frac {pi }{4}}=sin 45^{circ }=cos {frac {pi }{4}}=cos 45^{circ }={1 over {sqrt {2}}}={{sqrt {2}} over 2},,}$
${displaystyle tan {frac {pi }{4}}=tan 45^{circ }={{sin {frac {pi }{4}}} over {cos {frac {pi }{4}}}}={1 over {sqrt {2}}}cdot {{sqrt {2}} over 1}={{sqrt {2}} over {sqrt {2}}}=1.,}$

Computing trigonometric functions from an equilateral triangle

To determine the trigonometric functions for angles of $π$ /3 radians (60°) and $π$ /6 radians (30°), we start with an equilateral triangle of side length 1. All its angles are $π$ /3 radians (60°). By dividing it into two, we obtain a right triangle with $π$ /6 radians (30°) and $π$ /3 radians (60°) angles. For this triangle, the shortest side is 1/2the next largest side is √3/2 and the hypotenuse is 1. This yields:

${displaystyle sin {frac {pi }{6}}=sin 30^{circ }=cos {frac {pi }{3}}=cos 60^{circ }={1 over 2},,}$

${displaystyle cos {frac {pi }{6}}=cos 30^{circ }=sin {frac {pi }{3}}=sin 60^{circ }={{sqrt {3}} over 2},,}$

${displaystyle tan {frac {pi }{6}}=tan 30^{circ }=cot {frac {pi }{3}}=cot 60^{circ }={1 over {sqrt {3}}}={{sqrt {3}} over 3},.}$
Special values in trigonometric functions[edit]

There are some commonly used special values in trigonometric functions, as shown in the following table.

${displaystyle {begin{array}{|c|cccccccc|}{begin{matrix}{text{Radian}}\{text{Degree}}end{matrix}}&{begin{matrix}0\0^{circ }end{matrix}}&{begin{matrix}{frac {pi }{12}}\15^{circ }end{matrix}}&{begin{matrix}{frac {pi }{8}}\22.5^{circ }end{matrix}}&{begin{matrix}{frac {pi }{6}}\30^{circ }end{matrix}}&{begin{matrix}{frac {pi }{4}}\45^{circ }end{matrix}}&{begin{matrix}{frac {pi }{3}}\60^{circ }end{matrix}}&{begin{matrix}{frac {5pi }{12}}\75^{circ }end{matrix}}&{begin{matrix}{frac {pi }{2}}\90^{circ }end{matrix}}\hline sin &0&{frac {{sqrt {6}}-{sqrt {2}}}{4}}&{frac {sqrt {2-{sqrt {2}}}}{2}}&{frac {1}{2}}&{frac {sqrt {2}}{2}}&{frac {sqrt {3}}{2}}&{frac {{sqrt {6}}+{sqrt {2}}}{4}}&1\cos &1&{frac {{sqrt {6}}+{sqrt {2}}}{4}}&{frac {sqrt {2+{sqrt {2}}}}{2}}&{frac {sqrt {3}}{2}}&{frac {sqrt {2}}{2}}&{frac {1}{2}}&{frac {{sqrt {6}}-{sqrt {2}}}{4}}&0\tan &0&2-{sqrt {3}}&{sqrt {2}}-1&{frac {sqrt {3}}{3}}&1&{sqrt {3}}&2+{sqrt {3}}&infty \cot &infty &2+{sqrt {3}}&{sqrt {2}}+1&{sqrt {3}}&1&{frac {sqrt {3}}{3}}&2-{sqrt {3}}&0\sec &1&{sqrt {6}}-{sqrt {2}}&{sqrt {2}}{sqrt {2-{sqrt {2}}}}&{frac {2{sqrt {3}}}{3}}&{sqrt {2}}&2&{sqrt {6}}+{sqrt {2}}&infty \csc &infty &{sqrt {6}}+{sqrt {2}}&{sqrt {2}}{sqrt {2+{sqrt {2}}}}&2&{sqrt {2}}&{frac {2{sqrt {3}}}{3}}&{sqrt {6}}-{sqrt {2}}&1\end{array}}}$ ^[21]
The symbol $\infty$ here represents the point at infinity on the projectively extended real linethe limit on the extended real line is $+\infty$ on one side and $-\infty$ on the other.

Inverse functions[edit]

The trigonometric functions are periodic, and hence not injectiveso strictly they do not have an inverse function. Therefore, to define an inverse function we must restrict their domains so that the trigonometric function is bijective. In the following, the functions on the left are defined by the equation on the right; these are not proved identities. The principal inverses are usually defined as:

${displaystyle {begin{array}{rrc}{text{Function}}&{text{Definition}}&{text{Value Field}}\hline arcsin x=y&sin y=x&-{frac {pi }{2}}leq yleq {frac {pi }{2}}\arccos x=y&cos y=x&0leq yleq pi \arctan x=y&tan y=x&-{frac {pi }{2}}<y<{frac {pi }{2}}\operatorname {arccot} x=y&cot y=x&0<y<pi \operatorname {arcsec} x=y&sec y=x&0leq yleq pi ,,yneq {frac {pi }{2}}\operatorname {arccsc} x=y&csc y=x&-{frac {pi }{2}}leq yleq {frac {pi }{2}},,yneq 0end{array}}}$
The notations sin⁻¹ and cos⁻¹ are often used for arcsin and arccos, etc. When this notation is used, the inverse functions could be confused with the multiplicative inverses of the functions. The notation using the "arc-" prefix avoids such confusion, though "arcsec" for arcsecant can be confused with "arcsecond".
Just like the sine and cosine, the inverse trigonometric functions can also be defined in terms of infinite series. Zum Beispiel,

${displaystyle arcsin z=z+left({frac {1}{2}}right){frac {z^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {z^{5}}{5}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {z^{7}}{7}}+cdots ,.}$
These functions may also be defined by proving that they are antiderivatives of other functions. The arcsine, for example, can be written as the following integral:

${displaystyle arcsin z=int _{0}^{z}{frac {1}{sqrt {1-x^{2}}}},dx,quad |z|<1.}$
Analogous formulas for the other functions can be found at inverse trigonometric functions. Using the complex logarithmone can generalize all these functions to complex arguments:

${displaystyle {begin{aligned}arcsin z&=-ilog left(iz+{sqrt {1-z^{2}}}right),,\arccos z&=-ilog left(z+{sqrt {z^{2}-1}}right),,\arctan z&={frac {1}{2}}ilog left({frac {1-iz}{1+iz}}right).end{aligned}}}$
Connection to the inner product[edit]

In an inner product spacethe angle between two non-zero vectors is defined to be

${displaystyle operatorname {angle} (x,y)=arccos {frac {langle x,yrangle }{|x|cdot |y|}}.}$
Properties and applications[edit]

The trigonometric functions, as the name suggests, are of crucial importance in trigonometrymainly because of the following two results.

Law of sines[edit]

The law of sines states that for an arbitrary triangle with sides $a$ $b$ and $c$ and angles opposite those sides $A$ $B$ and $C$ :

${displaystyle {frac {sin A}{a}}={frac {sin B}{b}}={frac {sin C}{c}}={frac {2Delta }{abc}},}$
where $Δ$ is the area of the triangle,
or, equivalently,

${displaystyle {frac {a}{sin A}}={frac {b}{sin B}}={frac {c}{sin C}}=2R,}$
where $R$ is the triangle's circumradius.

It can be proven by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulationa technique to determine unknown distances by measuring two angles and an accessible enclosed distance.

Law of cosines[edit]

The law of cosines (also known as the cosine formula or cosine rule) is an extension of the Pythagorean theorem:

${displaystyle c^{2}=a^{2}+b^{2}-2abcos C,,}$
or equivalently,

${displaystyle cos C={frac {a^{2}+b^{2}-c^{2}}{2ab}}.}$
In this formula the angle at $C$ is opposite to the side $c$ . This theorem can be proven by dividing the triangle into two right ones and using the Pythagorean theorem.
The law of cosines can be used to determine a side of a triangle if two sides and the angle between them are known. It can also be used to find the cosines of an angle (and consequently the angles themselves) if the lengths of all the sides are known.

Law of tangents[edit]

The following all form the law of tangents^[22]

${displaystyle {frac {tan {dfrac {A-B}{2}}}{tan {dfrac {A+B}{2}}}}={frac {a-b}{a+b}},;qquad {frac {tan {dfrac {A-C}{2}}}{tan {dfrac {A+C}{2}}}}={frac {a-c}{a+c}},;qquad {frac {tan {dfrac {B-C}{2}}}{tan {dfrac {B+C}{2}}}}={frac {b-c}{b+c}}}$
The explanation of the formulae in words would be cumbersome, but the patterns of sums and differences, for the lengths and corresponding opposite angles, are apparent in the theorem.

Law of cotangents[edit]

If

${displaystyle zeta ={sqrt {{frac {1}{s}}(s-a)(s-b)(s-c)}} }$ (the radius of the inscribed circle for the triangle)
and

${displaystyle s={frac {a+b+c}{2}} }$ (the semi-perimeter for the triangle),
then the following all form the law of cotangents^[22]

${displaystyle cot {frac {A}{2}}={frac {s-a}{zeta }},;qquad cot {frac {B}{2}}={frac {s-b}{zeta }},;qquad cot {frac {C}{2}}={frac {s-c}{zeta }}}$
It follows that

${displaystyle {frac {cot {dfrac {A}{2}}}{s-a}}={frac {cot {dfrac {B}{2}}}{s-b}}={frac {cot {dfrac {C}{2}}}{s-c}}.}$
In words the theorem is: the cotangent of a half-angle equals the ratio of the semi-perimeter minus the opposite side to the said angle, to the inradius for the triangle.

Periodic functions[edit]

Sinusoidal basis functions (bottom) can form a sawtooth wave (top) when added. All the basis functions have nodes at the nodes of the sawtooth, and all but the fundamental ( $k = 1$ ) have additional nodes. The oscillation seen about the sawtooth when $k$ is large is called the Gibbs phenomenon

The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motionwhich models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion.
Trigonometric functions also prove to be useful in the study of general periodic functions. The characteristic wave patterns of periodic functions are useful for modeling recurring phenomena such as sound or light waves.^[23]
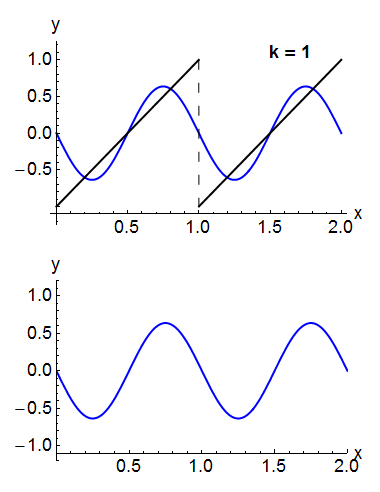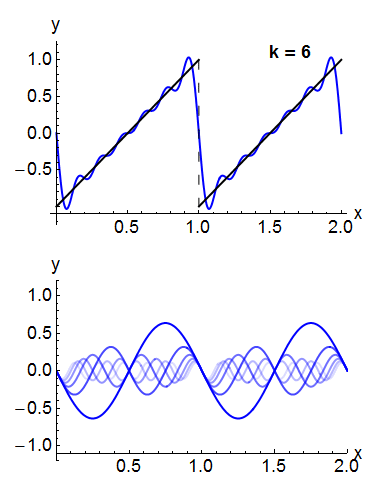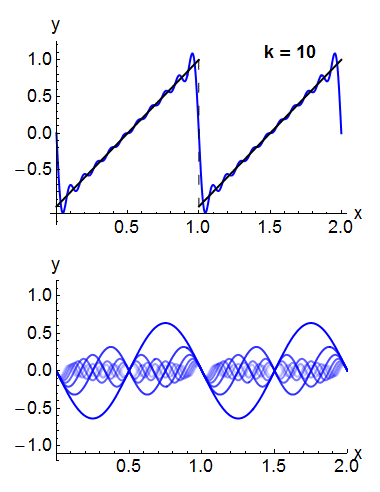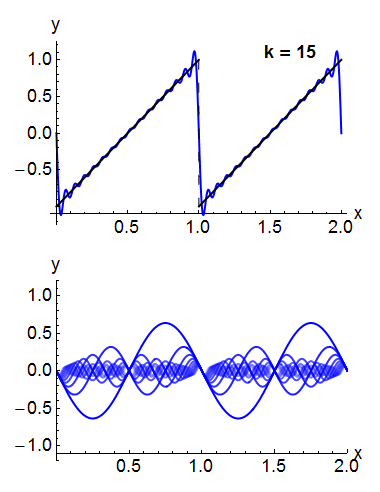
Under rather general conditions, a periodic function $f (x)$ can be expressed as a sum of sine waves or cosine waves in a Fourier series.^[24] Denoting the sine or cosine basis functions by $φ k$ the expansion of the periodic function $f (t)$ takes the form:

${displaystyle f(t)=sum _{k=1}^{infty }c_{k}varphi _{k}(t).}$
For example, the square wave can be written as the Fourier series

${displaystyle f_{text{square}}(t)={frac {4}{pi }}sum _{k=1}^{infty }{sin {big (}(2k-1)t{big )} over 2k-1}.}$
In the animation of a square wave at top right it can be seen that just a few terms already produce a fairly good approximation. The superposition of several terms in the expansion of a sawtooth wave are shown underneath.

History[edit]

While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Roman Egypt (90–165 CE).
The functions sine and cosine can be traced to the jyā and koti-jyā functions used in Gupta period Indian astronomy (AryabhatiyaSurya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin.^[25]
All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines, used in solving triangles.^[26]al-Khwārizmī produced tables of sines, cosines and tangents.
They were studied by authors including Omar Khayyám Bhāskara II Nasir al-Din al-Tusi Jamshīd al-Kāshī (14th century), Ulugh Beg (14th century), Regiomontanus (1464), Rheticusand Rheticus' student Valentinus Otho.
Madhava of Sangamagrama (c. 1400) made early strides in the analysis of trigonometric functions in terms of infinite series.^[27]
The terms tangent and secant were first introduced by the Danish mathematician Thomas Fincke in his book Geometria rotundi (1583).^[28]
The first published use of the abbreviations sincosand tan is probably by the 16th century French mathematician Albert Girard.^{[citation needed]}
In a paper published in 1682, Leibniz proved that $sin x$ is not an algebraic function of $x$ .^[29]
Leonhard Euler's Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting "Euler's formula", as well as near-modern abbreviations (sin.cos.tang.cot.sec.and cosec.).^[25]
A few functions were common historically, but are now seldom used, such as the chord ( $crd(θ) = 2 sin(θ / 2)$ ), the versine ( $versin(θ) = 1 - cos(θ) = 2 sin 2 (θ / 2)$ ) (which appeared in the earliest tables^[25]), the coversine ( $coversin(θ) = 1 - sin(θ) = versin(π / 2 - θ)$ ), the haversine ( $haversin(θ) = 1 / 2 versin(θ) = sin 2 (θ / 2)$ ),^[30] the exsecant ( $exsec(θ) = sec(θ) - 1$ ), and the excosecant ( $excsc(θ) = exsec(π / 2 - θ) = csc(θ) - 1$ ). See List of trigonometric identities for more relations between these functions.

Etymology[edit]

The word sine derives^[31] from Latin sinusmeaning "bend; bay", and more specifically "the hanging fold of the upper part of a toga", "the bosom of a garment", which was chosen as the translation of what was interpreted as the Arabic word jaibmeaning "pocket" or "fold" in the twelfth-century translations of works by Al-Battani and al-Khwārizmī into Medieval Latin.^[32]
The choice was based on a misreading of the Arabic written form j-y-b (جيب), which itself originated as a transliteration from Sanskrit jīvāwhich along with its synonym jyā (the standard Sanskrit term for the sine) translates to "bowstring", being in turn adopted from Ancient Greek χορδή "string".^[33]
The word tangent comes from Latin tangens meaning "touching", since the line touches the circle of unit radius, whereas secant stems from Latin secans—"cutting"—since the line cuts the circle.^[34]
The prefix "co-" (in "cosine", "cotangent", "cosecant") is found in Edmund Gunter's Canon triangulorum (1620), which defines the cosinus as an abbreviation for the sinus complementi (sine of the complementary angle) and proceeds to define the cotangens similarly.^[35]^[36]

See also[edit]

^ Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in German). 1 (3rd ed.). Berlin: J. Springer.

^ Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. ISBN 0-48643480-X. Archived from the original on 2018-02-15. Retrieved 2017-08-13.

^ Oxford English Dictionary, sine, n.²

^ Oxford English Dictionary, cosine, n.

^ Oxford English Dictionary, tangent, adj. and n.

^ Oxford English Dictionary, secant, adj. and n.

^ Heng, Cheng and Talbert, "Additional Mathematics" Archived 2015-03-20 at the Wayback Machinepage 228

^ Bityutskov, V.I. (2011-02-07). "Trigonometric Functions". Encyclopedia of Mathematics. Archived from the original on 2017-12-29. Retrieved 2017-12-29.

^ Larson, Ron (2013). Trigonometry (9th ed.). Lernen lernen. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 2018-02-15.Extract of page 153 Archived 2018-02-15 at the Wayback Machine

^ See Ahlfors, pages 43–44.

^ Abramowitz; Weisstein.

^ Stanley, Enumerative Combinatorics, Vol I., page 149

^ Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 2014-03-08.

^ Remmert, Reinhold (1991). Theory of complex functions. Springer p. 327. ISBN 0-387-97195-5. Archived from the original on 2015-03-20.Extract of page 327 Archived 2015-03-20 at the Wayback Machine

^ For a demonstration, see Euler's formula#Using power series

^ Needham, Tristan. Visual Complex Analysis. ISBN 0-19-853446-9.

^ Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer ISBN 978-0387894911.

^ Kantabutra.

^ However, doing that while maintaining precision is nontrivial, and methods like Gal's accurate tablesCody and Waite reduction, and Payne and Hanek reduction algorithms can be used.

^ Brent, Richard P. (April 1976). "Fast Multiple-Precision Evaluation of Elementary Functions". J. ACM. 23 (2): 242–251. doi:10.1145/321941.321944. ISSN 0004-5411.

^ Abramowitz, Milton and Irene A. Stegun, p.74

^ ^a ^b The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 529-530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.

^ Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publikationen. p. 82. ISBN 0-486-67620-X. Archived from the original on 2015-03-20.

^ See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). Amerikanische Mathematische Gesellschaft. pp. 77ff. ISBN 0-8218-4790-2. Archived from the original on 2015-03-19.

^ ^a ^b ^c Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. ISBN 0-471-54397-7p. 210.

^ Gingerich, Owen (1986). "Islamic Astronomy". 254. Scientific American: 74. Archived from the original on 2013-10-19. Retrieved 2010-07-13.

^ O'Connor, J. J.; Robertson, E. F. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. Archived from the original on 2006-05-14. Retrieved 2007-09-08.

^ "Fincke biography". Archived from the original on 2017-01-07. Retrieved 2017-03-15.

^ Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer.

^ Nielsen (1966pp. xxiii–xxiv)

^ The anglicized form is first recorded in 1593 in Thomas Fale's Horologiographia, the Art of Dialling.

^ Various sources credit the first use of sinus to either

See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and MechanismsSpringer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004.

^ See Plofker, Mathematics in IndiaPrinceton University Press, 2009, p. 257
See "Clark University". Archived from the original on 2008-06-15.
See Maor (1998), chapter 3, regarding the etymology.

^ Oxford English Dictionary

^ Gunter, Edmund (1620). Canon triangulorum.

^ Roegel, Denis, ed. (2010-12-06). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 2017-07-28. Retrieved 2017-07-28.

References[edit]

Abramowitz, Milton; Stegun, Irene Anneds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover-Publikationen. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.

Lars AhlforsComplex Analysis: an introduction to the theory of analytic functions of one complex variablesecond edition, McGraw-Hill Book CompanyNew York, 1966.

Boyer, Carl B.A History of MathematicsJohn Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.

Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).

Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics2nd ed. Penguin BooksLondon. (2000). ISBN 0-691-00659-8.

Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).

Maor, Eli, Trigonometric DelightsPrinceton Univ. Drücken Sie. (1998). Reprint edition (February 25, 2002): ISBN 0-691-09541-8.^{[dead link]}

Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.

Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York, USA: Barnes & Noble LCCN 61-9103

O'Connor, J. J., and E. F. Robertson, "Trigonometric functions"MacTutor History of Mathematics archive. (1996).

O'Connor, J. J., and E. F. Robertson, "Madhava of Sangamagramma"MacTutor History of Mathematics archive. (2000).

Pearce, Ian G., "Madhava of Sangamagramma"MacTutor History of Mathematics archive. (2002).

Weisstein, Eric W., "Tangent" from MathWorldaccessed 21 January 2006.

External links[edit]

Posted by yuaida ho87 at 12:21 PM
Email This BlogThis!Share to X Share to Facebook Share to Pinterest

No comments:

Post a Comment